Computer-Science

Public Key

1. Problem of symmetric-key algorithm

2. public-key algorithm

3. RSA

1) basic concepts

2) algorithm

3) security of RSA

n, e is known. Computing d from n and e is almost impossible. The number of bits of “n” is the key length of this RSA. 1024 bit is considered medium security.

4) using RSA

4. Usage of public-key system

1) digital signature by A

The receiver can check the validity of M by comparing its hash value with H(M). the H(M) can be obtained by decrypting enc(H(M), d_A) with e_A which is public.

If someone has changed M, the H(M) will not match. If someone, B, make a change in M and provide enc(H(M), d_B), the decryption with e_A will fail.

2) public key certificate (X. 509)

CA(Certificate Authority) : provide digital signature to a certificate

A person or an organization (company, web cite, …) can obtain a certificate from one of the CA’s. The CA verifies the information in the certificate and attaches a digital signature on it. X.509 specifies what information should be provided in the certificate.

X.509 file can be stored in various formats such as DER, PEM, cer, crt, PFX, …

ex) A certificate issued to “FreeSoft”. CA is “Thawte”

To confirm the validity of the above certificate, we need a certificate of Thawte.

5. Homework

3) Make an RSA key pair from two small prime numbers (p=11, q=3). Encrypt/decrypt for some example numbers. The example number should be in the range of 0 to 32. Try to encrypt HELLO using this RSA key.

4) Write a program that allows users to generate an RSA key and encrypt/decrypt with this key. Use the fact x*y mod n = (x mod n)*(y mod n) mod n

rsa.cpp :

#include <stdio.h>
#include <cmath>

int enc(int M, int e, int n);
int dec(int C, int d, int n);
int compute_pow(int a, int b, int m);
int select_e(int phi1, int p, int q);
int compute_phi2(int phi1);
int GCD(int a, int b);

int main()
{
	printf("enter p and q, two prime numbers\n");
	int p, q;
	scanf("%d %d", &p, &q);
	// step 1. compute n
	int n = p * q;
	// step 2. compute phi1
	int phi1 = (p - 1) * (q - 1);
	int e;
	int phi2;
	int d;

	for (;;)
	{
		// step 3. select e
		e = select_e(phi1, p, q);

		// step 4. compute phi2
		phi2 = compute_phi2(phi1);

		// step 5. compute d
		d = compute_pow(e, phi2 - 1, phi1);
		if (e == d)
			printf("not suitable e. select another one\n");
		else
		{
			printf("(%d %d) are ok to use ", e, d);
			break;
		}
	}
	printf("p:%d q:%d n:%d phi1:%d e:%d phi2:%d d:%d\n",
		   p, q, n, phi1, e, phi2, d);
	// now encrypt
	printf("enter num to encrypt\n");
	int M, C;
	scanf("%d", &M);
	C = enc(M, e, n);
	printf("M:%d C:%d\n", M, C);
	int Mp = dec(C, d, n);
	printf("Mp:%d\n", Mp);
}
int enc(int M, int e, int n)
{
	return compute_pow(M, e, n);
}
int dec(int C, int d, int n)
{
	return compute_pow(C, d, n);
}
int compute_pow(int a, int b, int m)
{
	unsigned long long int power = (unsigned long long int)pow(a, b);
	printf("%llu\n", power);
	return power % m; // return a^b mod m
}

int select_e(int phi1, int p, int q)
{
	printf("Choose 'e' and Enter one of the numbers below.\n");

	// display relative prime numbers to phi1
	for (int i = 2; i <= phi1 + 1; i++)
	{
		if (p % i == 0 or q % i == 0)
			continue;
		else
			printf("%d ", i);
	}
	// let user select one of them
	printf("\nSelect \'e\': ");

	int e;
	scanf("%d", &e);
	return e;
}

int compute_phi2(int phi1)
{
	int cnt = 0;
	for (int i = 1; i < phi1; i++)
	{
		if (GCD(phi1, i) == 1)
			cnt++;
	}
	return cnt; // return num of relative prime numbers to phi1
}

int GCD(int a, int b)
{
	int gcd;
	for (int i = 1; i <= a && i <= b; ++i)
	{
		// Checks if i is factor of both integers
		if (a % i == 0 && b % i == 0)
			gcd = i;
	}

	return gcd; // return GCD of a, b
}

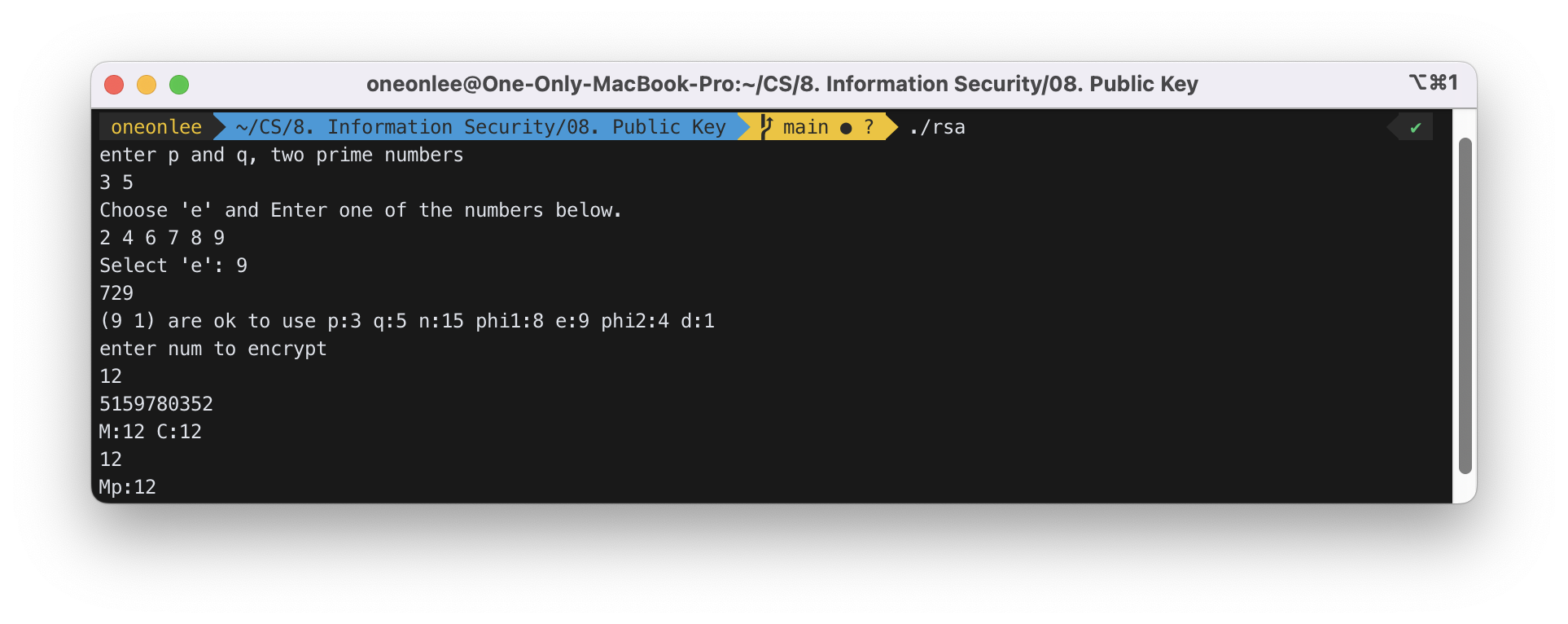
5) Write a program that breaks your RSA system.

6) Write a pair of secure client and server that exchange a password using RSA system.

7) Install openssl in your pc.

  1. download openssl from http://gnuwin32.sourceforge.net/packages/openssl.htm
    • (get “complete package except source”)
  2. install in your pc
  3. go to the installed directory/bin
  4. double click on openssl (you may need to run as “administrator”)

8-1) Generate an RSA key pair using openssl.

$ openssl
OpenSSL> genrsa -out mykey.pem 1024
    # generate public/private key pair in file "mykey.pem" with keysize 1024 bits.
    # default size 512 bits if keysize is not specified

8-2) Convert mykey.pem to a text file, mykey.txt, to look at the contents. Use WordPad to open mykey.txt. Find n, e, and d.

OpenSSL> rsa -in mykey.pem -text -out mykey.txt
    # display the contents of "mykey.pem" in plain text in
    # output file "mykey.txt"

8-3) Encrypt “hello” with (n, e) to produce ciphertext. How many bytes in the ciphertext? Decrypt the ciphertext with (n, d) to recover “hello”.

myplain.txt :

hello

OpenSSL> rsautl -encrypt -inkey mykey.pem -in myplain.txt -out mycipher # encrypting
OpenSSL> rsautl -decrypt -inkey mykey.pem -in mycipher -out mycipher.dec # decrypting

Refer the manual in man/pdf/openssl-mal.pdf.

PEM(Privacy Enhanced Mail) file format transforms a binary file into an ascii file using base64. Each 6 bit in the input file will be converted to a letter in {A-Z, a-z, 0-9, +, -}, and wrapped with boundary lines.
ex) Man ==> 77 97 110 ==> 01001101 01100001 01101110
==> T(010011, 19) W(010110, 22) F(000101, 5) u(101110, 46)

(.der : binary DER encoded certificates
.cer : similar to .der
.key : PKCS#8 keys. the keys are encoded as binary DER or ASCII PEM)

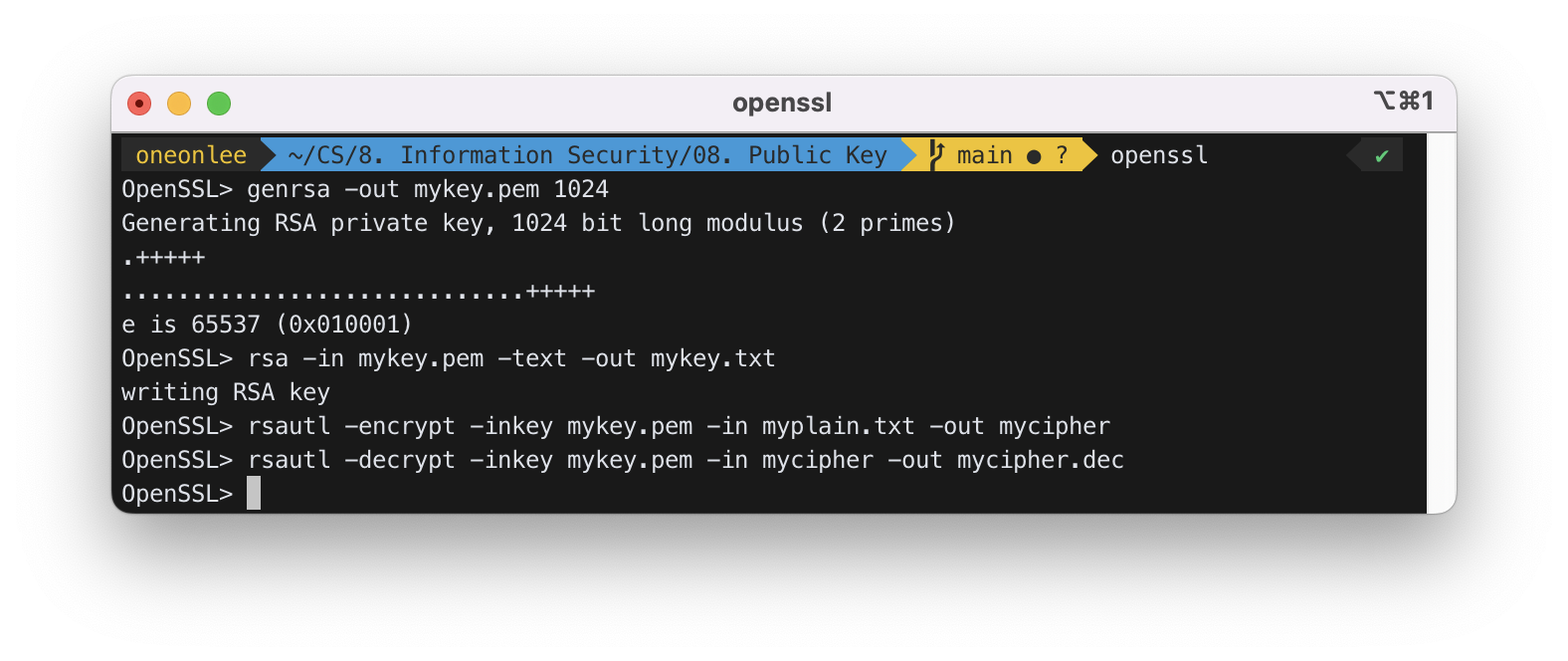
9) Make an X.509 certificate.

9.1) make a config file myconf.txt

myconf.txt :

[req]
string_mask = nombstr
distinguished_name = req_distinguished_name
prompt = no
[req_distinguished_name]
commonName = my CA
stateOrProvinceName = some state
countryName = US
emailAddress = root@somename.somewhere.com
organizationName = mycompany

9.2) Make a certificate for the person/company specified in myconf.txt. The public key of this person/company is given in mykey.pem:

OpenSSL> req -config myconf.txt -new -x509 -key mykey.pem -out mycert.pem

9.3) let’s read the contents of the certificate

OpenSSL> x509 -in mycert.pem -text -out mycert.txt

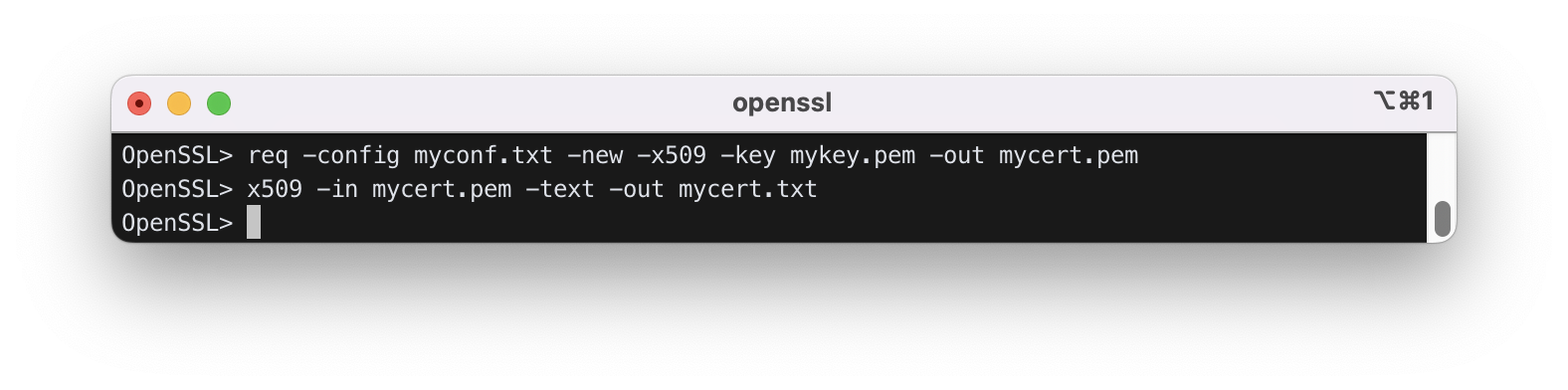
mycert.txt :

Certificate:
    Data:
        Version: 1 (0x0)
        Serial Number:
            47:c7:8c:3f:81:69:4d:b6:31:77:27:16:64:47:75:c9:8d:7d:2f:65
        Signature Algorithm: sha256WithRSAEncryption
        Issuer: CN = my CA, ST = some state, C = US, emailAddress = root@somename.somewhere.com, O = mycompany
        Validity
            Not Before: Nov  1 08:37:13 2022 GMT
            Not After : Dec  1 08:37:13 2022 GMT
        Subject: CN = my CA, ST = some state, C = US, emailAddress = root@somename.somewhere.com, O = mycompany
        Subject Public Key Info:
            Public Key Algorithm: rsaEncryption
                RSA Public-Key: (1024 bit)
                Modulus:
                    00:bf:f9:7f:75:7d:20:7f:2d:82:e5:29:93:80:3e:
                    61:d4:d1:78:47:2f:f5:1c:a6:7f:d2:d6:a9:bd:11:
                    81:c0:8a:ba:39:a2:d2:34:60:3f:99:8b:05:8d:cf:
                    04:60:e3:e2:de:a0:e0:83:d6:f7:ac:75:00:7d:c6:
                    73:38:41:cf:0c:f7:78:02:35:b6:f8:31:36:19:0d:
                    45:d7:83:2c:f9:cb:99:38:c7:d1:37:09:f3:a2:80:
                    2e:17:17:a8:36:da:70:74:2c:27:72:44:71:f8:64:
                    08:36:90:ad:0a:4a:30:a4:c1:3f:89:ad:b3:9c:12:
                    38:55:ca:37:32:5a:c6:aa:31
                Exponent: 65537 (0x10001)
    Signature Algorithm: sha256WithRSAEncryption
         25:b2:79:50:93:fe:3f:db:d3:c7:c8:69:79:b9:e9:96:12:38:
         da:17:88:1e:13:1f:01:aa:29:f3:21:3d:b0:45:cf:fe:c0:07:
         06:ae:76:a4:d2:29:7d:1e:3d:b3:be:65:0d:01:13:0c:8a:74:
         74:af:72:98:01:8b:e6:33:6c:6a:81:2c:e0:6f:8d:a4:eb:f6:
         df:76:4c:5b:62:60:4c:a5:48:63:d9:1c:31:6c:30:6c:df:c9:
         3f:92:e7:f9:56:94:21:5c:5b:a2:81:51:14:b9:65:2a:f0:e3:
         be:62:d9:ec:c6:51:4c:5d:b8:c7:7d:13:75:34:89:2c:00:fb:
         00:1a
-----BEGIN CERTIFICATE-----
MIICZjCCAc8CFEfHjD+BaU22MXcnFmRHdcmNfS9lMA0GCSqGSIb3DQEBCwUAMHIx
DjAMBgNVBAMTBW15IENBMRMwEQYDVQQIEwpzb21lIHN0YXRlMQswCQYDVQQGEwJV
UzEqMCgGCSqGSIb3DQEJARYbcm9vdEBzb21lbmFtZS5zb21ld2hlcmUuY29tMRIw
EAYDVQQKEwlteWNvbXBhbnkwHhcNMjIxMTAxMDgzNzEzWhcNMjIxMjAxMDgzNzEz
WjByMQ4wDAYDVQQDEwVteSBDQTETMBEGA1UECBMKc29tZSBzdGF0ZTELMAkGA1UE
BhMCVVMxKjAoBgkqhkiG9w0BCQEWG3Jvb3RAc29tZW5hbWUuc29tZXdoZXJlLmNv
bTESMBAGA1UEChMJbXljb21wYW55MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKB
gQC/+X91fSB/LYLlKZOAPmHU0XhHL/Ucpn/S1qm9EYHAiro5otI0YD+ZiwWNzwRg
4+LeoOCD1vesdQB9xnM4Qc8M93gCNbb4MTYZDUXXgyz5y5k4x9E3CfOigC4XF6g2
2nB0LCdyRHH4ZAg2kK0KSjCkwT+JrbOcEjhVyjcyWsaqMQIDAQABMA0GCSqGSIb3
DQEBCwUAA4GBACWyeVCT/j/b08fIaXm56ZYSONoXiB4THwGqKfMhPbBFz/7ABwau
dqTSKX0ePbO+ZQ0BEwyKdHSvcpgBi+YzbGqBLOBvjaTr9t92TFtiYEylSGPZHDFs
MGzfyT+S5/lWlCFcW6KBURS5ZSrw475i2ezGUUxduMd9E3U0iSwA+wAa
-----END CERTIFICATE-----

Who is the owner of this certificate? What is the public key? What is the key size?
Who has signed this certificate?

10) Get a certificate in Internet Explorer or in Chrome. Check the contents of x.509 file.

10.1) Go to “tools>internet options>contents>certificates” to get a copy of a certificate. To view the certificate of a site:


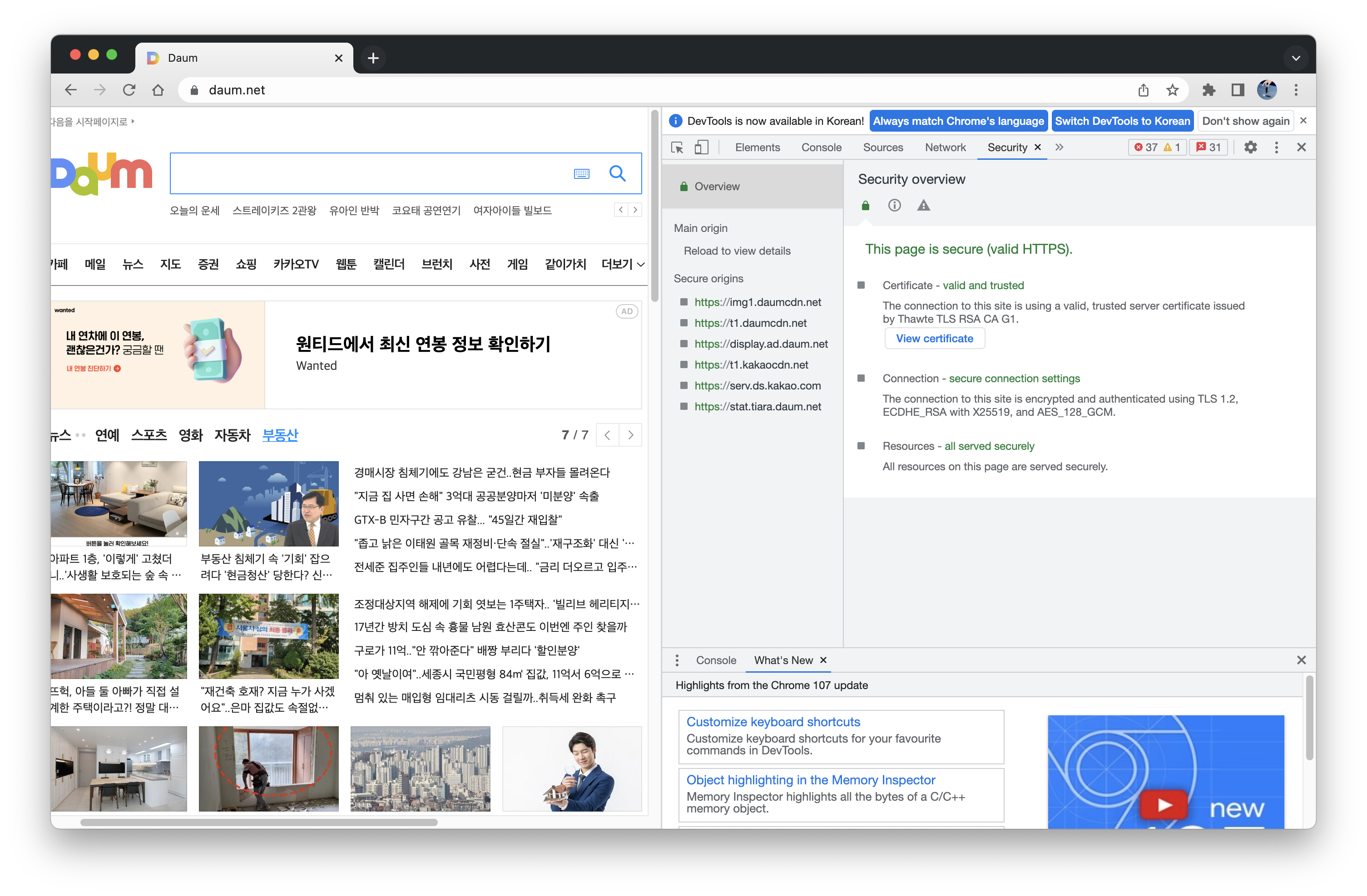
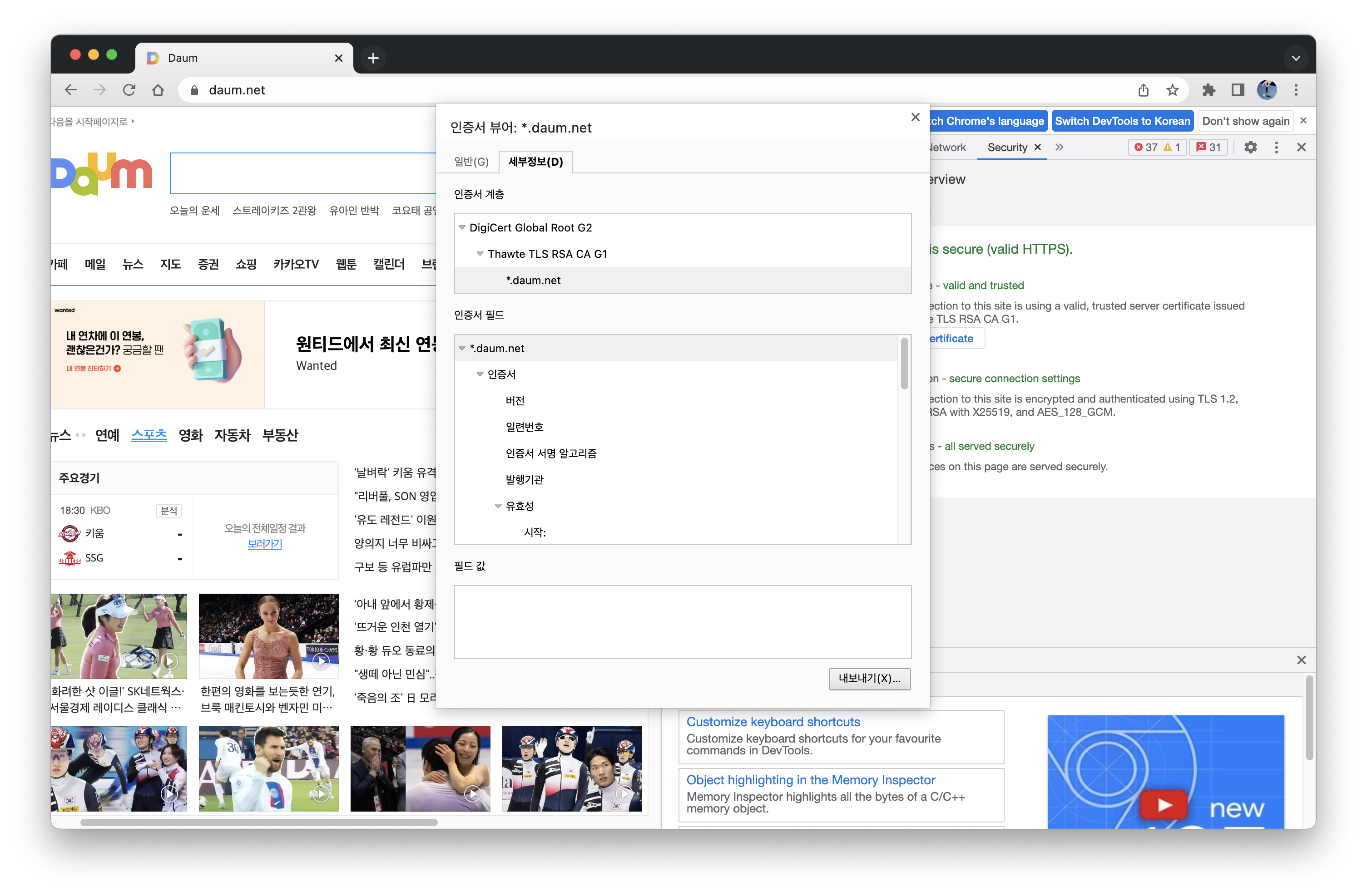
10.2) Look at the contents of this certificate (assume the file name is daum.cer) with

daum.cer :

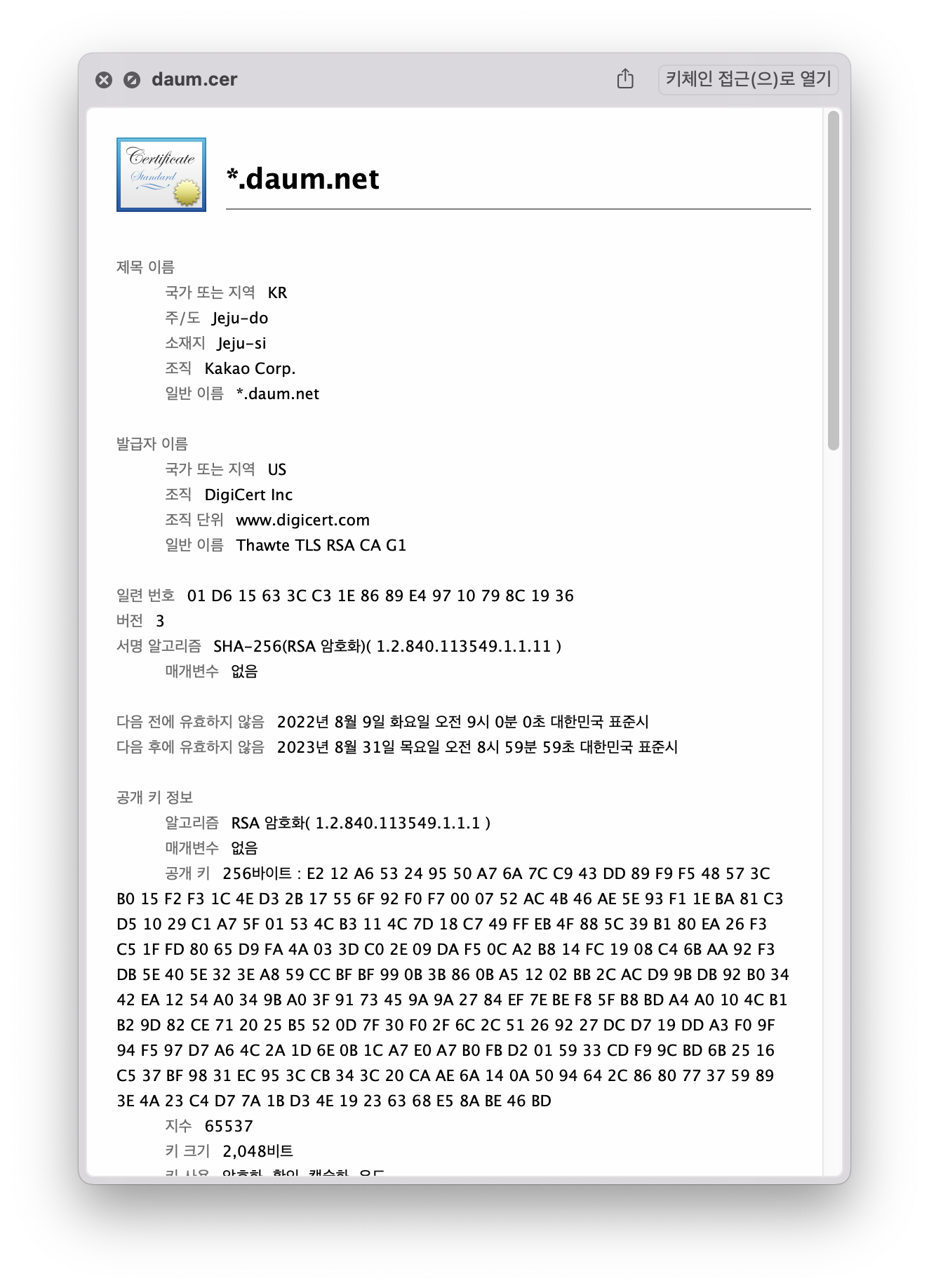
OpenSSL> x509 -in daum.cer -text -out daum.cer.txt -inform DER

(DER: Distinguished Encoding Rules)

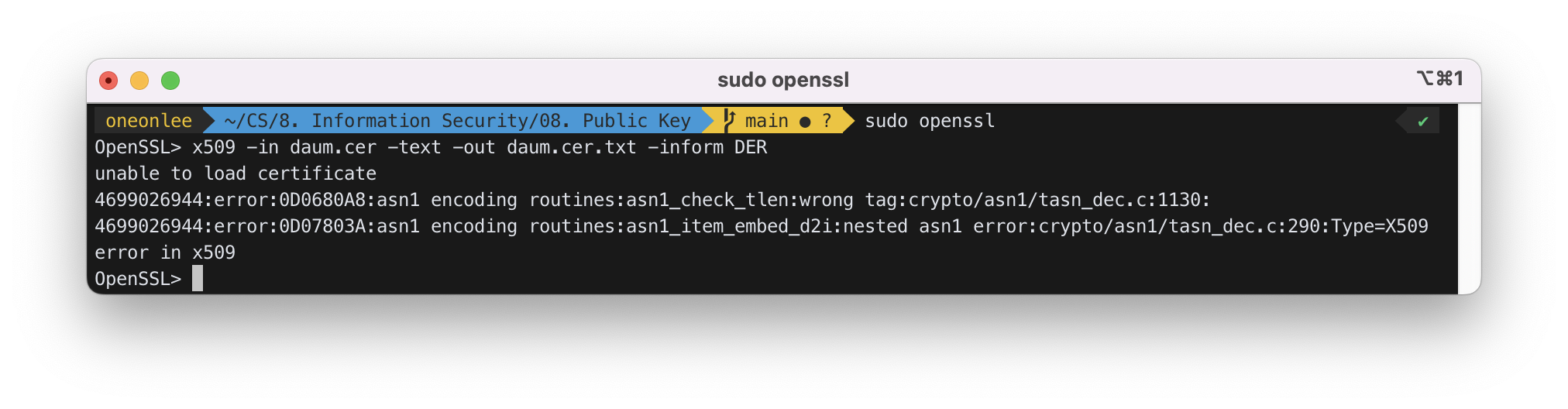
unable to load certificate
4699026944:error:0D0680A8:asn1 encoding routines:asn1_check_tlen:wrong tag:crypto/asn1/tasn_dec.c:1130:
4699026944:error:0D07803A:asn1 encoding routines:asn1_item_embed_d2i:nested asn1 error:crypto/asn1/tasn_dec.c:290:Type=X509
error in x509

위와 같은 에러가 발생하였다.

Who is the owner of this certificate? Who has signed this certificate? What is the public key?
What is the key size?

This site is open source. Improve this page.