Computer-Science
String Process Algorithm
Contents
스트링 탐색 알고리즘
- 문서 작성 시
- 텍스트(text) : 문서
- 패턴(pattern) : 탐색할 스트링
- 스트링(string)
- 문자가 연속적으로 나열된 것
- 텍스트(text) 스트링
- 이진(binary) 스트링
- 스트링 탐색 알고리즘의 설계 목적
- 필연적으로 잘못된 시작(false start) 발생
- (불일치가 발생한 위치까지 비교한 0개 이상의 문자를 의미)
- 잘못된 시작의 횟수와 길이를 줄이는 것
- 필연적으로 잘못된 시작(false start) 발생
직선적 알고리즘
aka. 무작정 무지성 알고리즘
- 한 글자 또는 한 비트씩 오른쪽으로 진행
- 텍스트의 처음부터 끝까지 모두 비교하며 탐색하는 알고리즘
Pseudo Code
BruteForce(p[], t[]) // 단순한 algo지만 직접 구현하면 어려울 수 있다.
M ← 패턴의 길이; N ← 텍스트의 길이;
for (i ← 0, j ← 0; j < M and i < N; i ← i + 1, j ← j + 1) do {
if (t[i] ≠ p[j]) then {
i ← i - j; // i가 1칸 이동
j ← -1;
}
}
if (j = M) then return i - M;
else return i;
end ButeForce()
시간복잡도
최악의 경우 시간 복잡도는 텍스트의 모든 위치에서 패턴을 비교해야 하므로 O(MN)이 됨
KMP 알고리즘
- KMP : Knuth, Morris and Pratt
- 불일치가 발생했을 경우 텍스트 스트링의 앞 부분에 어떤 문자가 있는지를 미리 알고 있다면, 불일치가 발생한 앞 부분에 대해서는 다시 비교하지 않고 매칭을 수행할 수 있음
- 패턴을 전처리하여 배열
next[M]을 구해서 잘못된 시작을 최소화함next[M]: 불일치가 발생했을 경우 이동할 다음 위치- 얼마만큼 점프할지 점프의 위츠를
next배열에 저장
- 얼마만큼 점프할지 점프의 위츠를
p[0~i]의 접미사와 일치한 최장 접두사의 끝자리 위치- 단, 최장접두사 != 전체문자열
시간 복잡도
O(M+N)
Pseudo Code: 재시작 위치 알고리즘
InitNext(p[])
M ← 패턴의 길이;
next[0] ← -1;
for (i ← 0, j ← -1; i < M; i ← i + 1, j ← j + 1) do
{
next[i] ← j;
while ((j ≥ 0) and (p[i] ≠ p[j])) do
j ← next[j];
}
end InitNext()
next[]의 의미next[i]는 주어진 문자열의 0~(i-1)까지의 부분 문자열 중에서 prefix == suffix가 될 수 있는 부분 문자열 중에서 가장 긴 것의 길이
Pseudo Code: KMP 알고리즘
KMP(p[], t[])
M ← 패턴의 길이; N ← 텍스트의 길이;
InitNext(p);
for(i←0,j←0; j <M and i<N; i←i+1,j←j+1) do
while ((j ≥ 0) and (t[i] ≠ p[j])) do
j ← next[j];
if (j = M) then return i - M;
else return i;
end KMP()
패턴이 내장된 KMP 알고리즘
- KMP 알고리즘을 위한 유한 상태 장치
- 유한 상태 장치 (finite state machine: FSM)
- 상태(state; 원으로 표시)
- 전이(transition; 선으로 표시)
- 일치 전이(match transition; 실선으로 표시) - 오른쪽으로 이동
- 불일치 전이(non-match transition; 점선으로 표시) - 왼쪽으로 이동
- 시작점 (왼쪽 끝의 사각형)
- 종료점 (오른쪽 끝의 사각형)
- 유한 상태 장치 (finite state machine: FSM)

- 개선된 유한 상태 장치
InitNext알고리즘의next[i] ← j;변경
if (p[i] == p[j]) then next[i] ← next[j];
else next[i] ← j

보이어-무어 알고리즘
- 오른쪽에서 왼쪽으로 스트링 탐색을 진행
- 불일치 문자 방책(mismatched character heuristic) 사용
- 텍스트에 있는 불일치가 발생한 문자가 패턴의 문자가 일치하도록 패턴을 오른쪽으로 이동
- 일치 접미부 방책(good suffix heuristic) 사용
- 패턴에서 불일치가 발생한 문자의 오른쪽에 있는 최대 접미부가 일치하도록 패턴을 오른쪽을 이동하는 것
- 두 방법 중 패턴을 우측으로 이동하는 거리가 더 긴 것을 선택
- 최선의 경우 시간 복잡도 :
O (m + n /m + |Σ|)- 알파벳이 큰 경우
O(m+n/m+|Σ|)시간에 수행될 가능성이 매우 높음
- 알파벳이 큰 경우
불일치 문자 방책과 일치 접미부 방책

Pseudo Code: 불일치 문자 방책 알고리즘
void InitSkip(char *p) {
int i, M = strlen(p);
for (i = 0; i < NUM; i++) skip[i] = M;
for (i = 0; i < M; i++) skip[index(p[i])] = M - i - 1;
}
MisChar(p[], t[])
M ← 패턴의 길이; N ← 텍스트의 길이;
InitSkip(p);
for (i ← M-1, j ← M-1; j ≥ 0; i ← i - 1, j ← j - 1) do
while (t[i] ≠ p[j]) do {
k ← skip[index(t[i])];
if (M-j > k) then i ← i + M - j; // M-j = 5-1 = 4
else i ← i + k; // k = 0
if (i ≥ N ) then return N;
j ← M - 1;
}
return i+1;
end MisChar()

라빈-카프 알고리즘
- 스트링을 숫자값으로 바꾼 다음 해시 값을 계산하여 매칭하는 알고리즘
- 최악의 시간 복잡도는
O(MN)이지만 평균적으로는 선형에 가까운 빠른 속도를 가지는 알고리즘
Levenshtein Distance 편집거리 알고리즘
패턴 매칭 알고리즘
패턴 매칭 (pattern matching)
- 텍스트 스트링에서 원하는 문자 패턴을 찾아 내는 것
- 패턴 기술
-
- 접합 (concatenation)
- 패턴에서 인접해 있는 두 문자가 텍스트에서 나타나면 매치
- 접합 (concatenation)
-
- 논리합 (or)
- 두 개의 문자 중 하나가 텍스트에 나타나면 매치
- 논리합 (or)
-
- 폐포 (closure)
- 특정한 문자가 0개 이상 나타나면 매치
- 폐포 (closure)
-

정규식 (regular expression)
- 특정한 규칙을 가진 문자열의 집합을 표현하는데 사용하는 형식 언어
- 세 가지 기본 연산들로 이루어진 심볼들의 스트링
- 심볼 (symbol)
*: 괄호 안에 있는 문자들이 0번 이상 나타남?: 어떤 문자와도 매치됨+: 또는 (or) 연산
- 심볼 (symbol)
- 예
?*(ie+ei)?*:ie또는ei를 가지고 있는 모든 단어(1+01)*(0+1): 연속적으로 두 개의0이 나오지 않는0과1로 이루어진 모든 스트링
패턴 매칭 장치 (pattern matching machine)
- 패턴 매칭에 사용되는 장치 패턴
- 결정적(deterministic) 장치
- 각각의 상태 전이가 다음 입력 문자에 의해 완전하게 결정되는 것
- 예 : KMP 알고리즘을 위한 유한 상태 장치
- 비결정적(nondeterministic) 장치
- 패턴을 매치하기 위해 하나 이상의 방법이 있을 경우, 장치가 올바른 것을 찾아 나가는 것
- 텍스트 스트링에서,
(A*B+AC)D와 같은 정규식을 찾는 경우 사용되며, 유일한 시작 상태와 종료 상태를 가진다.
패턴 매칭 장치 구현
- 장치를 구현하는데 가장 적합한 자료구조 : Deque[데크] (Double-Ended Queue)
- 스택과 큐의 특징을 조합
- 양방향에서 항목을 추가하는 것이 가능
- 입력은 양방향에서 가능
- 삭제는 데크의 처음에서만 가능한 ‘출력-제한 데크 (output-restricted deque)’ 사용
- <img src=”https://user-images.githubusercontent.com/73745836/171321018-3a604596-b32f-447a-8441-fa7e3243dfad.jpeg” width = 30%/>
동작 과정
- 개요
-
- 문자가 매치됨 → 새로운 상태를 데크의 끝에 삽입 (
insertLast)
- 문자가 매치됨 → 새로운 상태를 데크의 끝에 삽입 (
-
- 상태가 비어 있음 → 두 개의 가능한 상태를 데크의 처음에 삽입 (
insertionFirst)
- 상태가 비어 있음 → 두 개의 가능한 상태를 데크의 처음에 삽입 (
-
scan을 만남 → 입력 스트링에 대한 포인터를 다음 문자로 이동
-
- 종료 조건
- 입력의 끝까지 갔을 때 (매치되지 않음)
- 상태 0을 만남 (매치됨)
- 데크에
scan마크 하나만 남음 (매치되지 않음)
<img src=”https://user-images.githubusercontent.com/73745836/171323280-63ef8485-dd51-483a-8c14-61671bfe78d8.jpeg” width = 60%/>
파일 압축 알고리즘
허프만 인코딩 (Huffman encoding)
with Priority Queue
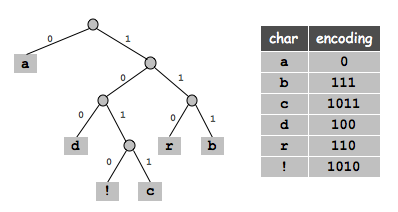
알고리즘
- 모든 노드를 PQ에
insert한다. - freq가 가장 작은 두 노드를 PQ에서 빼온다.
- 그 두 노드를 하나의 노드로 묶는다.
- 하나로 묶은 노드를 다시 PQ에 넣는다.
- 2번 ~ 4번의 과정을 계속 반복한다.
암호화 알고리즘
공개 키 암호화 시스템
RSA(Rivest-Shamir-Adleman) 알고리즘
-
- 서로 다른 두 개의 큰 소수
p,q선택 (100자리)p*q → r
- 서로 다른 두 개의 큰 소수
-
- 하나의 큰 숫자
e선택 (공개 암호화 키)p-1,q-1과 각각 서로소이어야 함p,q보다 큰 어떤 소수이어햐 함
- 하나의 큰 숫자
-
- 비밀 해독키
d계산(e*d) % {(p-1)*(q-1)} == 1을 만족하는d찾기- 표기법 :
d*e = 1 modulo (p-1)*(q-1)mod연산에 대한 표기법 참고
- 비밀 해독키
-
- 정수
r과e는 공개하고,d는 비밀로 유지
- 정수
-
- 평문
P로부터 암호문C = P^e modulo r계산
- 평문
-
- 암호문
C로부터 평문P = C^d modulo r계산
- 암호문
>>> p = 3
>>> q = 5
>>> r = p*q
>>> r
15
>>> (p-1)*(q-1)
8
>>>
>>> # let e be 11 (prime greater than both p, q)
>>> e = 11
>>>
>>> # find d
>>> # d*e = 1 modulo (p-1)*(q-1)
>>> # d*11 = 1 modulo 8
>>> # so, d = 3
>>> d = 3
>>>
>>> ## Encryption ###
>>> # let P = 13 (Plain text)
>>> P = 13
>>> # C = P^e modulo r
>>> # C = P**e % r
>>> # C = 13*11 % 15
>>> C = P**e % r
>>> C
7
>>>
>>> ### Decryption ###
>>> # P = C^d modulo r
>>> # P = C**d % r
>>> # P = 7**3 % 15
>>> P = C**d % r
>>> P
13
발송인 S가 수신인 R에게 메시지 P 전송
발송인 S :
수신인 R :
S가 메시지 P를 전송하였다는 것을 확인할 수 있음!